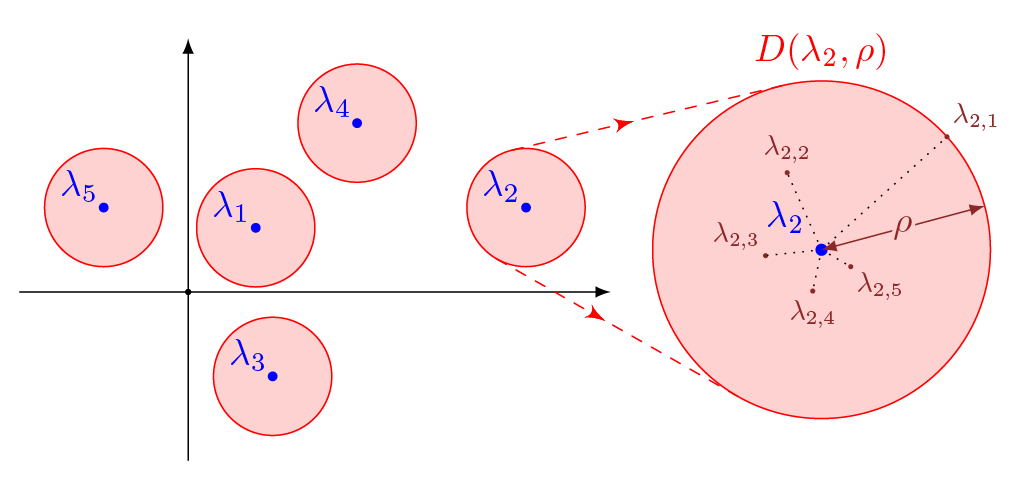
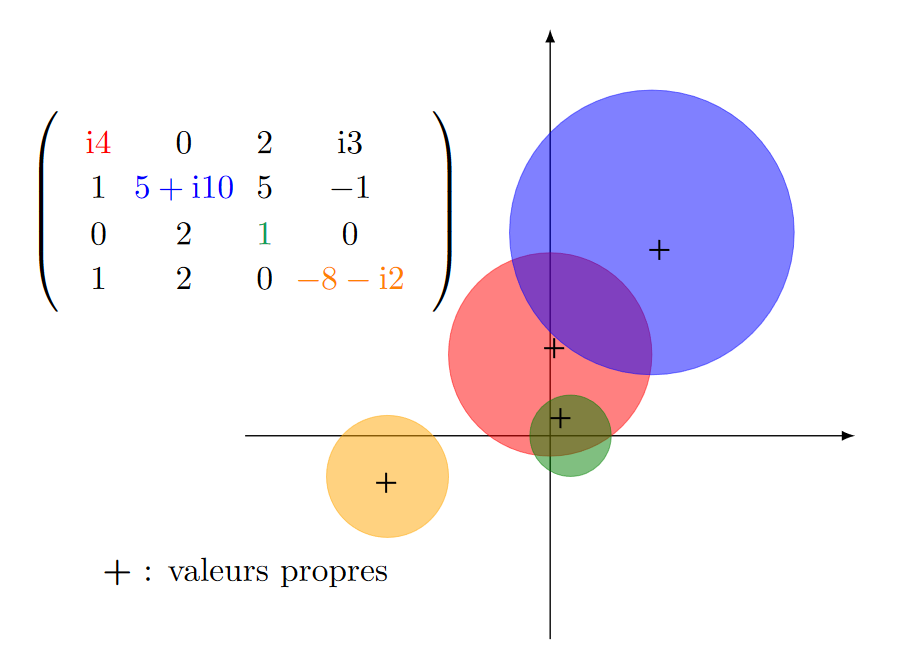
Soit \(M \in \mathscr{M}_n(\mathbb{C})\). Cette matrice est trigonalisable puisque son polynôme caractéristique est scindé sur \(\mathbb{C}\) d'après le théorème de d'Alembert-Gauss. On note \(\lambda_1\), ..., \(\lambda_s\) ses valeurs propres distinctes et \(r_1\), ..., \(r_s\) les multiplicités associées. Il existe donc une matrice \(P \in \mathrm{GL}_n(\mathbb{C})\) telle que $$ M = P \begin{pmatrix} \lambda_1 & & & t_{i,j} \\ 0 & \ddots & & \\ \vdots & \ddots & \ddots & \\ 0 & \cdots & 0 & \lambda_s \end{pmatrix} P^{-1} = P T P^{-1}. $$ Soit \(\varepsilon > 0\), nous allons commencer par "séparer" les valeurs propres distinctes. On peut trouver un rayon \(\rho\) tel que \(0 < \rho < \varepsilon\), pour lequel les disques \(D(\lambda_1, \rho)\), ..., \(D(\lambda_s, \rho)\) sont distincts deux à deux. Enfin, dans chacun de ces disques - qui sont des parties infinies de \(\mathbb{C}\) - on peut, pour tout \(i \in [\![ 1\,; s ]\!]\), choisir \(r_i\) complexes notés \(\lambda_{i,1}\), ..., \(\lambda_{i,r_i}\) distincts deux à deux. On peut même expliciter $$\lambda_{i,1} = \lambda_i + \frac{\rho}{1}, \dots, \lambda_{i, r_i} = \lambda_i + \frac{\rho}{r_i}.$$ On considère alors la matrice $$M_\varepsilon = P \begin{pmatrix} \lambda_{1, 1} & & & t_{i,j} \\ 0 & \ddots & & \\ \vdots & \ddots & \ddots & \\ 0 & \cdots & 0 & \lambda_{s, r_s} \end{pmatrix} P^{-1} = P T_\varepsilon P^{-1}. $$ Par construction, cette matrice de \(\mathscr{M}_n(\mathbb{C})\) possède \(n\) valeurs propres distinctes, elle est donc diagonalisable. On choisit maintenant sur \(\mathscr{M}_n(\mathbb{C})\) la norme du \(\sup\) sur les coefficients, définie par: $$\forall M = (m_{i,j})_{1 \leqslant i, j \leqslant n} \in \mathscr{M}_n(\mathbb{C}),\ \Vert M \Vert = \max_{1 \leqslant i, j \leqslant n} |m_{i,j}|.$$ On démontre facilement que pour \(A, B \in \mathscr{M}_n(\mathbb{C})\), \(\Vert AB \Vert \leqslant n \Vert A \Vert \Vert B \Vert\). Ainsi $$\Vert M - M_\varepsilon \Vert = \left\Vert P (T - T_\varepsilon) P^{-1} \right\Vert \leqslant \underbrace{n \Vert P \Vert \left\Vert P^{-1} \right\Vert}_{= K} \Vert T - T_\varepsilon \Vert \leqslant K \varepsilon.$$ En effet, $$ T - T_\varepsilon = \begin{pmatrix} \lambda_1 - \lambda_{1, 1} & & \\ & \ddots & \\ & & \lambda_s - \lambda_{s, r_s} \end{pmatrix} $$ donc $$\Vert T - T_\varepsilon \Vert = \max\limits_{1 \leqslant i \leqslant n} |\lambda_i - \lambda_{i, r_i}|.$$ Or les \(\lambda_{i, r_i}\) ont été choisis dans les disques \(D(\lambda_i, \rho)\) et donc pour tout \(i \in [\![ 1\,; n ]\!]\), $$\big|\lambda_i - \lambda_{i, r_i}\big| \leqslant \rho < \varepsilon.$$ Ceci achève la démonstration, puisque si \(\varepsilon\) tend vers \(0\), la matrice \(M_\varepsilon\) tend vers la matrice \(M\) pour la norme \(\Vert \cdot \Vert\) donc pour toute norme puisqu'en dimension finie, toutes les normes sont équivalentes.